The Riemann Sum Formula For the Definite Integral

The Riemann Sum formula provides a precise definition of the definite integral as the limit of an infinite series. The Riemann Sum formula is as follows:

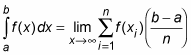
Below are the steps for approximating an integral using six rectangles:

1. Increase the number of rectangles (n) to create a better approximation:

   
   
   



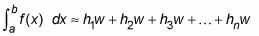
2. Simplify this formula by factoring out w from each term:

   
   
   



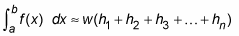
3. Use the summation symbol to make this formula even more compact:

   
   
   

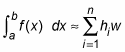
   The value w is the width of each rectangle:

   
   
   

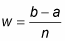
   Each h value is the height of a different rectangle:

   
   
   

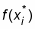
   So here is the Riemann Sum formula for approximating an integral using n rectangles:

   
   
   



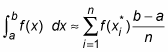
4. For a better approximation, use the limit

   
   
   



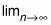
5. to allow the number of rectangles to approach infinity:

   
   
   

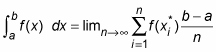
dummies

Source:http://www.dummies.com/how-to/content/the-riemann-sum-formula-for-the-definite-integral.html