How to Break Down a Composition of Functions

A composition of functions is one function acting upon another. Think of it like putting one function inside of the other — f (g (x)), for instance, means that you plug the entire g (x) function into f (x). To solve such a problem, you work from the inside out:

In the following examples, let

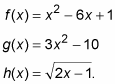
Then,

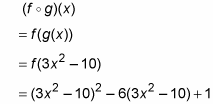
This process puts the g (x) function into the f (x) function everywhere the f (x) function asks for x. This equation ultimately simplifies to

in case you’re asked to simplify the composition.

Likewise,

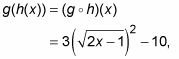
which easily simplifies to 3(2x – 1) – 10 because the square root and square cancel each other. This equation simplifies even further to 6x – 13.

You can’t just square the square root in the combined function h (g (x)) without stating that the domain is restricted because its domain controls the domain of the composed function. Although the composition seems like it should be linear, and therefore have a domain of all real numbers, in fact it does not. If you simply don’t square out the square root, the domain becomes clear: [0.5, ∞). But the graph doesn’t look like a square-root graph or a quadratic; it looks like a line that starts at x = 1/2. So, don’t simplify the equation unless you specify that the domain is now restricted.

You may also be asked to find one value of a composed function. To find

for instance, it helps to realize that it’s like reading Hebrew: You work from right to left. In this example, you’re asked to put –3 into f (x), get an answer, and then plug that answer into g (x). Here are these two steps in action:

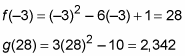
dummies

Source:http://www.dummies.com/how-to/content/how-to-break-down-a-composition-of-functions.html